Composing profunctors

The composite \(\mathcal{X}\overset{\phi;\psi}\nrightarrow \mathcal{Z}\) of two \(\mathcal{V}\) profunctors, \(\mathcal{X}\overset{\phi}\nrightarrow\mathcal{Y}\) and \(\mathcal{Y}\overset{\psi}\nrightarrow\mathcal{Z}\)

\((\phi;\psi)(x,z) = \bigvee_Y(\phi(x,y)\otimes\psi(y,z))\)

Linked by

• Exercise 4-22: referenced
• V-profunctor category: referenced
• Proof: referenced
• Exercise 4-31: referenced

• Need a formula for composing two feasibility relations in series.

• Suppose \(P,Q,R\) are cities (preorders) and there are bridges (hence, feasibility matrices).

• 

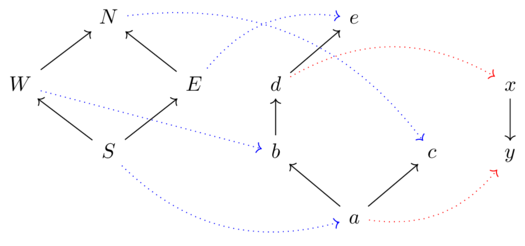
• The feasibility matrices are:

  \(\textcolor{blue}{\phi}\)	a	b	c	d	e
  N	T	F	T	F	F
  E	T	F	T	F	T
  W	T	T	T	T	F
  S	T	T	T	T	T

  \(\textcolor{red}{\psi}\)	x	y
  a	F	T
  b	T	T
  c	F	T
  d	T	T
  e	F	F

• Feasibility from \(P\) to \(R\) means there is a way-point in Q which is both reachable from \(p \in P\) and can reach \(r \in R\).

• Composition is ?a union \((\phi;\psi)(p,r):= \bigvee_Q \phi(p,q)\land \psi(q,r)\).

• But this is tantamount to ?matrix multiplication which gives us the result matrix:

  \(\phi;\psi\)	x	y
  N	F	T
  E	F	T
  W	T	T
  S	T	T

Consider the following Cost profunctors \(\textcolor{blue}{\phi},\textcolor{red}{\psi}\) \[\begin{tikzcd}[ampersand replacement=\&] A \arrow[d, "3"', bend right] \& B \arrow[l, "2"', bend right] \arrow[d, "5", bend left] \arrow[r, "11", blue, dotted, bend left] \& x \arrow[rr, "3", bend left] \arrow[rd, "4", bend left] \& \& z \arrow[ld, "4", bend left] \arrow[r, "4", red,dotted, bend left] \arrow[rd, red, "4", dotted, bend right] \& p \arrow[r, "2", bend left] \& q \arrow[d, "2", bend left] \\ C \arrow[ru, "3"] \& D \arrow[l, "4", bend left] \arrow[rr, blue, "9", dotted, bend right] \& \& y \arrow[lu, "3", bend left] \arrow[rrr, red, "0", dotted, bend right=49] \& \& d \arrow[u, "1", bend left] \& r \arrow[l, "1", bend left] \end{tikzcd}\]

Fill in the matrix for the composite profunctor.

Solution(1)

\(\phi;\psi\)	p	q	r	s
A	23	25	21	22
B	17	19	15	16
C	20	22	18	19
D	11	13	9	10